The following example is a generic product pricing problem, in which the goal is to set a price for each product p \in P, with P a set of products. The objective function is the maximization of profitability, which is not only a function of price itself, but also of the sensitivity of customers to the proposed price. And this is where the non-linearity comes into play.
Price sensitivity is typically captured as a function with the following characteristics.
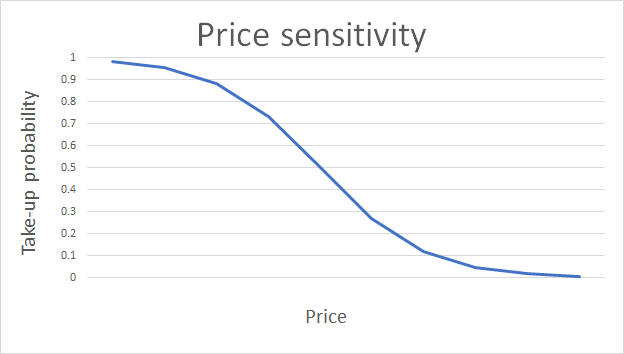
For a low price, the probability of a customer buying the product, referred to as the take-up probability, is expected to be high. However, when the price is too high, a low take-up is anticipated. By incorporating this non-linear relationship into the product pricing problem, more appropriate prices are determined.
Instead of determining actual prices for products, let x_p be a continuous variable which denotes the profit margin of a product p \in P. This is just easier to work with and we don’t have to concern ourselves with cost data as well. Let f_p(x_p) be the profit (price) sensitivity function for each product p \in P.
The only data we still need to complete the problem formulation is, the maximum attainable profit \pi_p, the maximum production capacity c_p, and the minimum allowable production volume v_p.
The objective of the product pricing problem is to maximize total profit by taking price sensitivity into account. This is achieved by first, expressing the unit profit of each product as \pi_px_p, and secondly expressing the total production volume as c_pf_p(x_p). By multiplying these two terms, the formulation of the product pricing problem is
Maximize~ \sum\limits_{p \in P}{\pi_{p}x_pc_pf_p(x_p)}
\\c_{p}f_p(x_p) \geq v_{p},\qquad\forall p \in PThe only constraint we consider for this problem formulation, is to ensure that the expected product take-up, as a result of the prescribed price, is more than the allowable minimum production volume.
We follow a well-known linearization approach based on a SOS type II formulation, to solve this problem as a mixed integer linear programming problem. First, the non-linear function f_p(x_p) is approximated by piece-wise linear segments. The linear segment intersections are represented by the graph points (xp_g, tp_g), with g \in G.
Using the x-axis points xp_g with g \in G, we can now generate graph points (xp_g, yp_g), with yp_g = \pi_px_pc_pf_p(x_p) for the purpose of approximating the objective function.
Recall from the initial non-linear formulation above, we defined the decision variable x_p as the profit margin of a product p \in P. Let t_p be the corresponding take-up probability and let y_p be the corresponding profit, for the product p \in P.
In addition, the auxiliary variables \lambda_{pg} \in [0,1] and s_{pg}, with p \in P and g \in G, are required to formulate the linearized product pricing problem:
\begin{array}{cl} Maximize~ \sum\limits_{p \in P}{y_{p}}& \\x_{p}= \sum\limits_{g \in G}{xp_{g} \lambda_{p,g}},\qquad\forall p \in P& :1\\t_{p}= \sum\limits_{g \in G}{tp_{p,g} \lambda_{p,g}},\qquad\forall p \in P& :2\\y_{p}= \sum\limits_{g \in G}{yp_{p,g} \lambda_{p,g}},\qquad\forall p \in P& :3\\ \sum\limits_{g \in G}{\lambda_{p,g}}=1,\qquad\forall p \in P& :4\\\lambda_{p,1} \leq s_{p,2},\qquad\forall p \in P& :5\\\lambda_{p,g} \leq s_{p,g}+s_{p,g+1},\qquad\forall p \in P,g \in G \setminus \{1,|G| \}& :6\\\lambda_{p,|G|-1} \leq s_{p,|G|},\qquad\forall p \in P& :7\\ \sum\limits_{g \in G \setminus \{1 \}}{s_{p,g}}=1,\qquad\forall p \in P& :8\\c_{p} t_{p} \geq v_{p},\qquad\forall p \in P& :9\\ \end{array}Constraint 1-4, ensure that the decision variables x_p, t_p, and y_p, are expressed as convex combinations of the graph points (xp_g, tp_g) and (xp_g, yp_g), respectively. Constraints 5-8 ensure that the correct line segment is selected as part of the linearization step, and constraint 9 ensures that the total product take-up is sufficient to satisfy the minimum volume requirements.
For the purpose of this example, the following function was used to create a fictitious price sensitivity graph for each product p \in P:
f_p(x_p)=\frac{1}{1+exp(-\alpha_p+\beta_px_p)}The two curve parameters, \alpha_p and \beta_p, is part of the input data provided in the Excel file pricing.xlsx.
The following is the complete code listing for the product pricing problem:
model pricing
set P = load_products()
set G = load_graph_points()
const v = load_min_prod(), forall p in P
const c = load_max_prod(), forall p in P
const xp = load_standardized_profit(), forall g in G
const yp = load_expected_profit(), forall p in P, forall g in G
const tp = load_takeup_percentages(), forall p in P, forall g in G
var 0 <= y <= 100000000, forall p in P
var 0 <= x <= 1, forall p in P
var 0 <= t <= 1, forall p in P
var 0 <= lambda <= 1, forall p in P, forall g in G
bin s, forall p in P, forall g in G
max sum_{p in P}{ y_{p} }
constr x_{p} = sum_{g in G}{ xp_{g}*lambda_{p,g} }, forall p in P
constr t_{p} = sum_{g in G}{ tp_{p,g}*lambda_{p,g} }, forall p in P
constr y_{p} = sum_{g in G}{ yp_{p,g}*lambda_{p,g} }, forall p in P
constr sum_{g in G}{ lambda_{p,g} } = 1, forall p in P
constr lambda_{p,1} <= s_{p,2}, forall p in P
constr lambda_{p,g} <= s_{p,g} + s_{p,g+1}, forall p in P, forall g in G setminus {1,|G|}
constr lambda_{p,|G|-1} <= s_{p,|G|}, forall p in P
constr c_{p}*t_{p} >= v_{p}, forall p in P
end
import elytica
import pandas
import math
xls = pandas.ExcelFile("pricing.xlsx")
data_sheet = xls.parse("data")
products = data_sheet["Product"].to_list()
max_prof = {i:j for i,j in zip(data_sheet["Product"], data_sheet["MaxProfit"])}
max_prod = {i:j for i,j in zip(data_sheet["Product"], data_sheet["MaxProd"])}
min_prod = {i:j for i,j in zip(data_sheet["Product"], data_sheet["MinProd"])}
alpha = {i:j for i,j in zip(data_sheet["Product"], data_sheet["alpha"])}
beta = {i:j for i,j in zip(data_sheet["Product"], data_sheet["beta"])}
nof_gpoints = 10
graph_points = [t for t in range(1,nof_gpoints+1)]
xp = {g:g/nof_gpoints for g in graph_points}
tp = {p:{g: 1/(1+math.exp(-alpha[p] + beta[p]*xp[g])) for g in graph_points} for p in products}
yp = {p:{g: max_prof[p]*xp[g] * max_prod[p]*tp[p][g] for g in graph_points} for p in products}
def load_products():
return products
def load_graph_points():
return graph_points
def load_min_prod():
return min_prod
def load_max_prod():
return max_prod
def load_standardized_profit():
return xp
def load_expected_profit():
return yp
def load_takeup_percentages():
return tp
def main():
elytica.init_model("pricing")
elytica.run_model("pricing")
P = elytica.get_model_set("pricing", "P")
result = [["product", "price"]]
for p in P:
vname = "x"+str(p)
val = elytica.get_variable_value("pricing", vname)
print(vname, val)
row = []
row.append( p )
row.append( val )
result.append( row )
excel={'excel': {'solution': result }}
elytica.write_results(json.dumps(excel))
return 0
