The input to a resource constrained scheduling problem (RCSP) is a set of activities I, where each activity i \in I has a duration d_i and consumes a unit v_{ir} of a resource r \in R, per time period. Typically, the order in which these activities may be scheduled, is determined by a precedence graph. The nodes of this directed graph represent the various activities and each arc a precedence relationship. For the purpose of this exercise, we will be ignoring the precedence requirements and only focus on the resource requirements.
The scheduling of the activities is performed to optimize a specific objective function, e.g. net present value (NPV). For this purpose, a cash flow c_i, is associated with each activity i \in I. The output produced by solving the RCSP, is a schedule indicating the start time of each activity.

The numbering on the activities in the above Gantt chart, shows the consumption of a specific resource during each time period. For a feasible solution to exist, the total resource consumption per time period must be less than or equal to the available resources. For this example, the sum over all the resources consumed per period is less than 15, which was provided as the capacity constraint for this example.
Let \rho be the discount factor to be applied in the calculation of the NPV, and let u_r be the resource capacity of a resource r \in R, per time period. Then the formulation of the RCSP when maximizing NPV is the following:
\text{maximize} \sum_{i \in I}\sum_{t \in T}{ \frac{c_ix_{it}}{(1+\rho)^t}}
\\\sum_{t \in T}{x_{it}} = 1, \forall i \in I
\\\sum_{i \in I}\sum_{k = t}^{ t+d_i -1 } v_{ir}x_{ik}\le u_r , \forall r \in R, \forall t \in TAs part of this example, we want to read the input data for the RCSP from an Excel file. First, we populate the sheets of the Excel file, named scheduling.xlsx, as follows:
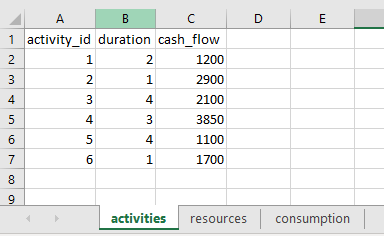
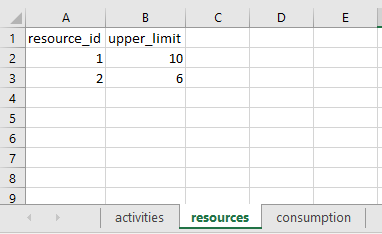
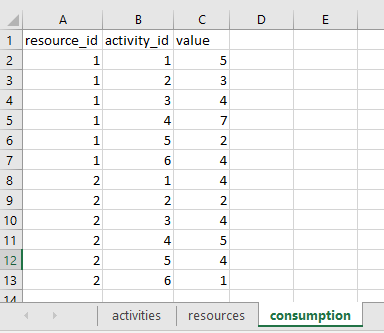
Now, you need to upload the file scheduling.xlsx, to the elytica platform. After opening your newly created project, click on  to upload the file.
to upload the file.
From the above problem formulation of the RCSP, it is clear that we will be reading in data for several sets and constants. But before we get started, let us first prepare our project by removing some of the default code (knapsack example) in our newly created project. The following code listing is a template of an “empty” project.
model rcsp
end
import elytica
import pandas
def main():
elytica.init_model("rcsp")
print("Completed")
return 0
By systematically adding code to this project, you will be able to inspect the reading in of data from the Excel file, by printing it to the output panel of the editor. For instance, let us start with reading in the set of activities. First, the following code is added just after the import pandas statement, and before the definition of the main function.
xls="scheduling.xlsx"
activity_sheet = json.loads((pd.read_excel(xls, sheet_name = "activities")).to_json(orient='records'))
activities = [i["activity_id"] for i in activity_sheet]
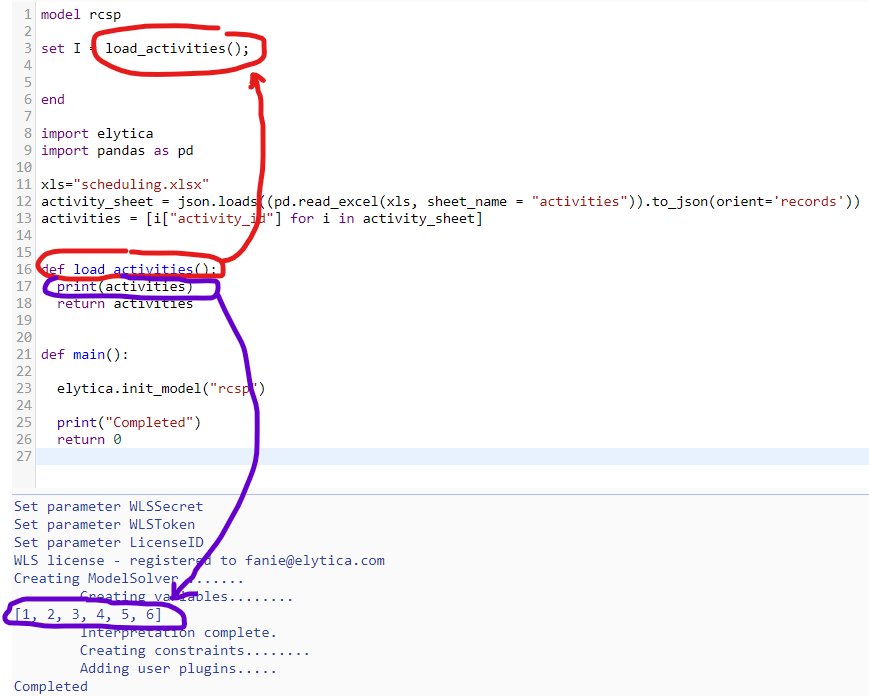
print(activities) Now we have the activity id’s stored in a Python list. The print statement is just to validate what we have been reading from the Excel file. To transfer this list into our model we need to add the following function
def load_activities():
return activitiesThe function can now be called within the mathematical model to populate the set of activities, as indicated below:
Reading in the remaining sets are done in a similar way. Now, let us start with reading in the constants. From the mathematical formulation, each activity has a duration d_i. We make use of a Python dictionary for this purpose.
durations = {i["activity_id"]:i["duration"] for i in activity_sheet}
def load_durations():
return durationsThe activity durations can now be made available to the mathematical model by calling the function load_durations():
const d = load_durations(), forall i in IReading in the rest of the one-dimensional constant arrays, e.g. resource limits u_r, are done in a similar fashion. Reading in multi-dimensional arrays, e.g. the resource consumption values v_{ir}, requires a bit more effort – we need to create a two-dimensional Python dictionary. Although we realize that there may be various ways of doing this, we opted for the following:
resource_values = {i["activity_id"]: {r["resource_id"]: r["value"] for r in consumption_sheet if r["activity_id"] == i["activity_id"]} for i in consumption_sheet}
def load_resource_values():
return resource_valuesTo access the resource values in the mathematical model, you have to add the following statement:
const v = load_resource_values(), forall i in I, forall r in RNote that the function load_resource_values() are followed by two forall statements, indicating the the constant v_{ir} will be indexed by both an activity index i, and a resource index r.
Reading in the cash flows c_i is treated differently, since we will be applying a discounted cash flow in the formulation of the objective function. That is, instead of explicitly capturing the NPV formula as part of the objective function, we introduce the constant
dc_{i,t}=\frac{c_i}{(1+\rho)^t}which is the discounted cash flow for an activity i \in I, and time period t \in T. If we assume a NPV discount rate of \rho=10\%, The following Python code will produce the required two-dimensional dictionary:
def load_discounted_cf():
return {i : {t : cash_flows[i]/(1.1)**t for t in time_periods } for i in activities}
Accessing the discounted cash flow in the mathematical model, requires the following statement:
const dc = load_discounted_cf(), forall i in I, forall t in TThe following code listing finalizes the reading of the data, without solving any model yet.
model rcsp
set I = load_activities()
set T = load_time_periods()
set R = load_resources()
const d = load_durations(), forall i in I
const u = load_resource_limits(), forall r in R
const v = load_resource_values(), forall i in I, forall r in R
const dc = load_discounted_cf(), forall i in I, forall t in T
end
import elytica
import pandas as pd
xls="scheduling.xlsx"
activity_sheet = json.loads((pd.read_excel(xls, sheet_name = "activities")).to_json(orient='records'))
resource_sheet = json.loads((pd.read_excel(xls, sheet_name = "resources")).to_json(orient='records'))
consumption_sheet = json.loads((pd.read_excel(xls, sheet_name = "consumption")).to_json(orient='records'))
activities = [i["activity_id"] for i in activity_sheet]
durations = {i["activity_id"]:i["duration"] for i in activity_sheet}
cash_flows = {i["activity_id"]:i["cash_flow"] for i in activity_sheet}
time_periods = list(range(1, sum( durations )))
resources = [r["resource_id"] for r in resource_sheet]
resource_limits = {r["resource_id"]:r["upper_limit"] for r in resource_sheet}
resource_values = {i["activity_id"]: {r["resource_id"]: r["value"] for r in consumption_sheet if r["activity_id"] == i["activity_id"]} for i in consumption_sheet}
def load_activities():
return activities
def load_time_periods():
return time_periods
def load_resources():
return resources
def load_durations():
return durations
def load_resource_limits():
return resource_limits
def load_resource_values():
return resource_values
def load_discounted_cf():
return {i : {t : cash_flows[i]/(1.1)**t for t in time_periods } for i in activities}
def main():
elytica.init_model("rcsp")
return 0
We now get to the formulation of the RCSP problem. First, the declaration of the decision variables and the objective function, in terms of the discounted cash flow values, are the following:
bin x, forall i in I, forall t in T
max sum_{t in T}{ sum_{i in I}{ dc_{i,t}*x_{i,t} }}
The first constraint, which ensures that each activity will be scheduled to start some time during the scheduling horizon, is
constr sum_{t in T}{ x_{i,t} } = 1, forall i in IThe following set of resource capacity constraints, ensures that the total resource consumption per time period is less than the available resources. The formulation of this constraint is written mathematically as
\\\sum_{i \in I}\sum_{k = t}^{ t+d_i -1 } v_{ir}x_{ik}\le u_t , \forall r \in R,\forall t \in TSince we make use of a set-based approach in capturing mathematical models, we will reformulate this constraint by using the subset \delta(i,t) \subseteq T:
\sum_{i \in I}{ \sum_{k \in \delta(i,t) }{ v_{i,r}x_{i,k} }} <= u_{r}, \forall t \in T, \forall r \in RThat is, the subset \delta(i,t) filters out the required time period indices, based on the current activity i \in I, and current time period t \in T.
The use of the subset \delta(i,t) \subseteq T in the constraint formulation requires you to add the following to the model declaration (with all the other set loading statements)
set delta(I,T) = load_delta()The corresponding Python implementation of the load function is then
def load_delta():
return {i : {t : [ k for k in time_periods if k >= t and k <= t + durations[i] - 1] for t in time_periods } for i in activities}In this tutorial, a data-driven approach is following in setting up the model. That is, all input data (sets and constants), are read from a data source and the size of the problem instance is not known in advance. To accommodate the printing of the solutions in a similar manner, the function elytica.get_model_set is provided to access the elements of a set outside the scope of the mathematical model. Have a look at the bottom of the following code listing to see how we use this for printing the final solution.
model rcsp
set I = load_activities()
set T = load_time_periods()
set R = load_resources()
set delta(I,T) = load_delta()
const d = load_durations(), forall i in I
const u = load_resource_limits(), forall r in R
const v = load_resource_values(), forall i in I, forall r in R
const dc = load_discounted_cf(), forall i in I, forall t in T
bin x, forall i in I, forall t in T
max sum_{t in T}{ sum_{i in I}{ dc_{i,t}*x_{i,t} }}
constr sum_{t in T}{ x_{i,t} } = 1, forall i in I
constr sum_{i in I}{ sum_{k in delta(i,t) }{ v_{i,r}*x_{i,k} }} <= u_{r}, forall t in T, forall r in R
end
import elytica
import pandas as pd
xls="scheduling.xlsx"
activity_sheet = json.loads((pd.read_excel(xls, sheet_name = "activities")).to_json(orient='records'))
resource_sheet = json.loads((pd.read_excel(xls, sheet_name = "resources")).to_json(orient='records'))
consumption_sheet = json.loads((pd.read_excel(xls, sheet_name = "consumption")).to_json(orient='records'))
activities = [i["activity_id"] for i in activity_sheet]
durations = {i["activity_id"]:i["duration"] for i in activity_sheet}
cash_flows = {i["activity_id"]:i["cash_flow"] for i in activity_sheet}
time_periods = list(range(1, sum( durations )))
resources = [r["resource_id"] for r in resource_sheet]
resource_limits = {r["resource_id"]:r["upper_limit"] for r in resource_sheet}
resource_values = {i["activity_id"]: {r["resource_id"]: r["value"] for r in consumption_sheet if r["activity_id"] == i["activity_id"]} for i in consumption_sheet}
def load_activities():
return activities
def load_time_periods():
return time_periods
def load_resources():
return resources
def load_durations():
return durations
def load_resource_limits():
return resource_limits
def load_resource_values():
return resource_values
def load_discounted_cf():
return {i : {t : cash_flows[i]/(1.1)**t for t in time_periods } for i in activities}
def load_delta():
return {i : {t : [ k for k in time_periods if k >= t and k <= t + durations[i] - 1] for t in time_periods } for i in activities}
def main():
elytica.init_model("rcsp")
elytica.run_model("rcsp")
I = elytica.get_model_set("rcsp", "I")
T = elytica.get_model_set("rcsp", "T")
for i in I:
for t in T:
vname = "x"+str(i)+","+str(t)
val = elytica.get_variable_value("rcsp", vname)
if val > 0 :
print("activity ", i, " starts at time ", t )
return 0
