The input to a traveling salesman problem is a set of nodes (cities) N and a distance matrix. The objective is to find a route of minimum distance, which will allow a traveling salesman to visit each node exactly once.

The formulation we present here for solving the traveling salesman problem is a more compact formulation which assumes an incomplete graph, with a set of edges E – i.e. links without direction. The major benefit of doing this is that we don’t have to specify a complete distance matrix like we’ve done with the Shortest Path example in Tutorial 3. Now, we only need to specify the distances for the existing links, i.e., for each e \in E, the distance is given by d_e.
To allow the use of edges (no direction) instead of arcs (with direction), we introduce functions \alpha(e) and \beta(e), which retrieve the end-nodes of a specified edge e \in E. Furthermore, Let \sigma(i) \subseteq N be the set of adjacent nodes to a node i \in N. We will give more detail on how to configure these functions when presenting the example below.
The decision variable x_{ij}, will take on a value of 1 if the arc from node i \in N to node j \in N, is part of the solution which will minimize the total distance traveled. The corresponding formulation of the traveling salesman is the following:
\begin{array}{cl} Minimize~ \sum\limits_{e \in E}{d_{e} x_{\alpha(e),\beta(e)}+d_{e} x_{\beta(e),\alpha(e)}}& \\ \sum\limits_{j \in \sigma(i)}{x_{i,j}}=1,\qquad\forall i \in N& \\ \sum\limits_{j \in \sigma(i)}{x_{j,i}}=1,\qquad\forall i \in N& \\u_{i}-u_{j}+|N| x_{i,j} \leq |N|-1,\qquad\forall i \in N \setminus \{1 \},j \in \sigma(i) \setminus \{1 \}& \\u_{n} \leq |N|-1,\qquad\forall n \in N \setminus \{1 \}& \\u_{n} \geq 1,\qquad\forall n \in N \setminus \{1 \}& \\ \end{array}The first two constraints allow a node to be visited only once, and the remaining constraints are the subtour elimination constraints (Miller–Tucker–Zemlin formulation).
We will use the following example to take you through the steps in formulating the Traveling Salesman problem:
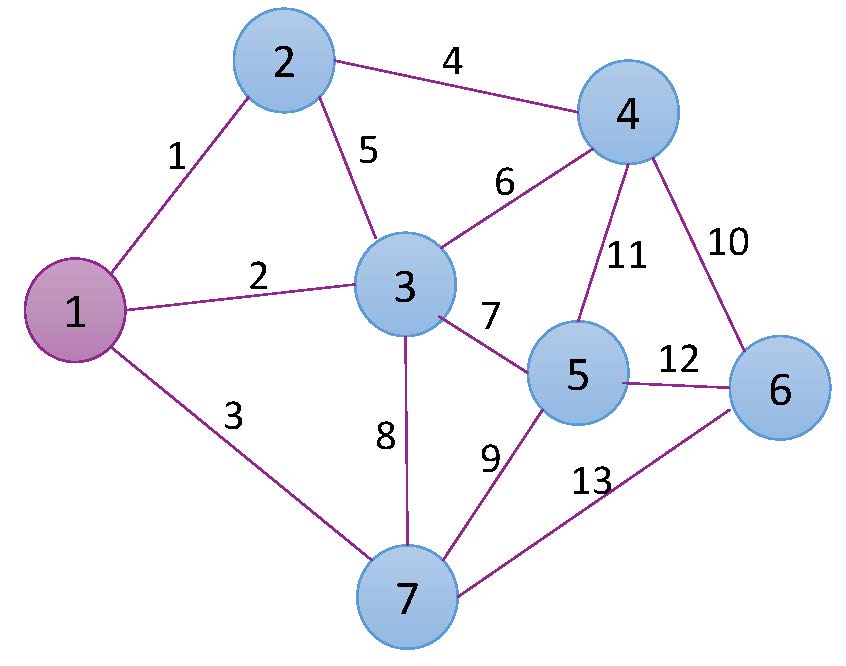
The numbering alongside each link is to uniquely identify each edge. The set of nodes and edges that we will use in the subsequent formulation are then defined as:
set N = {1,2,3,4,5,6,7}
set E = {1,2,3,4,5,6,7,8,9,10,11,12,13}
To define the subset \sigma(i) \subseteq N, which is the set of adjacent nodes to a node i \in N, we add the following statement:
set sigma(N) = load_sigma()Intuitively, the statement indicates that the subset \sigma is obtained by filtering on the set N, based on a node index from the set N. Note that load_sigma() is a custom Python function that returns a dictionary indexed by the set N. The implementation of this function is added below the model block and looks like this:
def load_sigma():
S = {1: [2,3,7], 2: [1,3,4], 3: [1,2,4,5,7], 4: [2,3,5,6], 5: [3,4,6,7], 6: [4,5,7], 7: [1,3,5,6]}
return SThe dictionary S contains for each node a set of adjacent nodes, e.g., the first key in the dictionary is node 1 in our example, and the adjacent nodes are 2, 3 and 7.
Next, the edge distances are given by
const d = {5,3,6,4,4,3,1,2,3,1,3,1,2}, forall e in Eand the decision variable by
bin x, forall i in N, forall j in N
int 0<= u <= infty, forall n in N
Note that this is the first time that we’ve been using integer variables, which is defined by using the int keyword. Note that variable bounds have to accompany the declaration of integer variables (as well as continuous variables which are define by the var keyword)
The formulation of the objective function requires the functions \alpha(e) and \beta(e), which retrieve the end-nodes of a specified edge e \in E. The implementation of these functions is as follows:
def alpha(e):
A = {1:1, 2:1, 3:1, 4:2, 5:2, 6:3, 7:3, 8:3, 9:5, 10:4, 11:4, 12:5, 13:7}
return A[int(e)]
def beta(e):
B = {1:2, 2:3, 3:7, 4:4, 5:3, 6:4, 7:5, 8:7, 9:7, 10:6, 11:5, 12:6, 13:6}
return B[int(e)]
The dictionary defined in \alpha contains the one end-node for a given edge, and the dictionary defined in \beta contains the other end-node for the same edge. For example, the end-node for edge 1 according to \alpha is the node 1, and the other end-node according to \beta is the node 2.
The objective function, expressed in terms of edge indices, is
min sum_{e in E}{ d_{e}*x_{alpha(e), beta(e)} + d_{e}*x_{beta(e), alpha(e)}}Note that, although the decision variable x_{ij} is defined in terms of the node indices i \in N and indices i \in N, the use of the functions \alpha and \beta means that only the variables that correspond to existing edges, are included in the model formulation.
The complete code listing of the Traveling Salesman is as follows:
model ts
set N = {1,2,3,4,5,6,7}
set E = {1,2,3,4,5,6,7,8,9,10,11,12,13}
set sigma(N) = load_sigma()
const d = {5,3,6,4,4,3,1,2,3,1,3,1,2}, forall e in E
bin x, forall i in N, forall j in N
int 0<= u <= infty, forall n in N
min sum_{e in E}{ d_{e}*x_{alpha(e), beta(e)} + d_{e}*x_{beta(e), alpha(e)}}
constr sum_{j in sigma(i)}{ x_{i,j} } = 1, forall i in N
constr sum_{j in sigma(i)}{ x_{j,i} } = 1, forall i in N
constr u_{i} - u_{j} + |N|*x_{i,j} <= |N|-1, forall i in N setminus {1}, forall j in sigma(i) setminus {1}
constr u_{n} <= |N|-1, forall n in N setminus {1}
constr u_{n} >= 1, forall n in N setminus {1}
end
import elytica as e
def load_sigma():
S = {1: [2,3,7], 2: [1,3,4], 3: [1,2,4,5,7], 4: [2,3,5,6], 5: [3,4,6,7], 6: [4,5,7], 7: [1,3,5,6]}
return S
def alpha(e :int):
A = {1:1, 2:1, 3:1, 4:2, 5:2, 6:3, 7:3, 8:3, 9:5, 10:4, 11:4, 12:5, 13:7}
return A[e]
def beta(e :int):
B = {1:2, 2:3, 3:7, 4:4, 5:3, 6:4, 7:5, 8:7, 9:7, 10:6, 11:5, 12:6, 13:6}
return B[e]
def main():
e.init_model("ts")
e.run_model("ts")
N = e.get_model_set("ts", "N")
[print(f"{i} -> {j}") for i in N for j in N if e.get_variable_value("ts", f"x{i},{j}") > 0.5]
[print(f"n {i} {v}") for i in N if (v := e.get_variable_value("ts", f"u{i}"))]
return 0
