In this blog post, we will build on the model of the previous tutorial and introduce the use of index sets when formulating an optimization problem. The benefit of using index-based variables are realized when you start to work with a large number of variables, or if you want to generalize your optimization model for any problem size.
Logging in and starting your project
Use your elytica credentials and log into https://compute.elytica.com . The following screen should appear and display the project that you created as part of Tutorial 1, namely, the Knapsack project:
By clicking on “Knapsack” you will be transferred to the editor screen of the project we created as part of Tutorial 1.
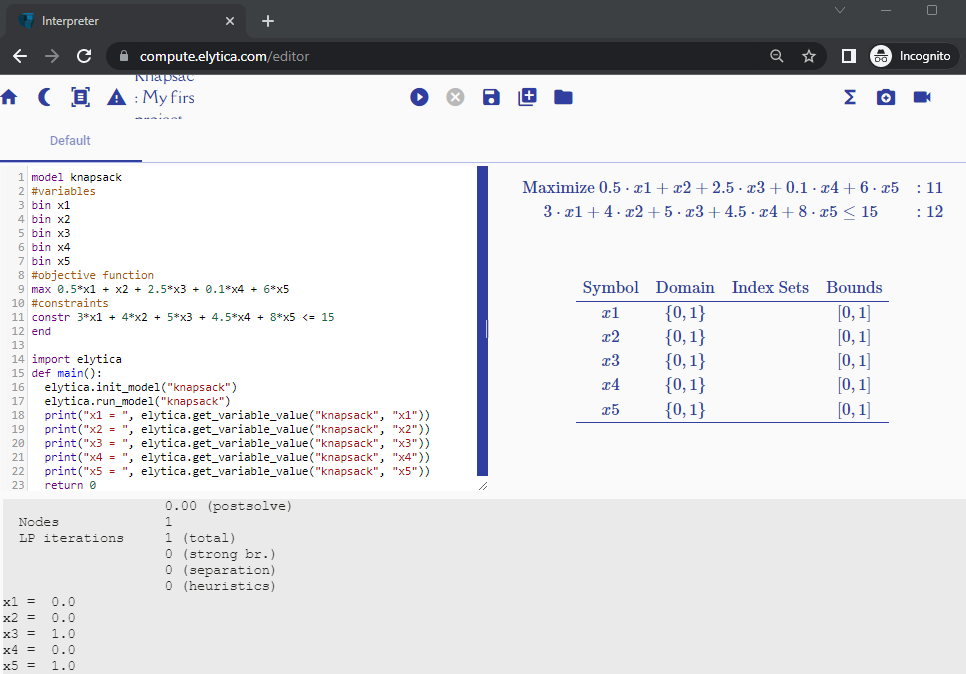
You will now add a new “job” to your project by clicking on ![]() (part of the center group of icons). If you type in “Index-based variables” as the name of the new job and select the “Knapsack (set-based version)” template, the following tab will appear in the editor:
(part of the center group of icons). If you type in “Index-based variables” as the name of the new job and select the “Knapsack (set-based version)” template, the following tab will appear in the editor:
Once again, by pressing the run button ![]() you should see output appear on the right-hand side of the screen (rendering of the mathematical model), as well as the bottom of the screen (output produced by solving the optimization problem):
you should see output appear on the right-hand side of the screen (rendering of the mathematical model), as well as the bottom of the screen (output produced by solving the optimization problem):
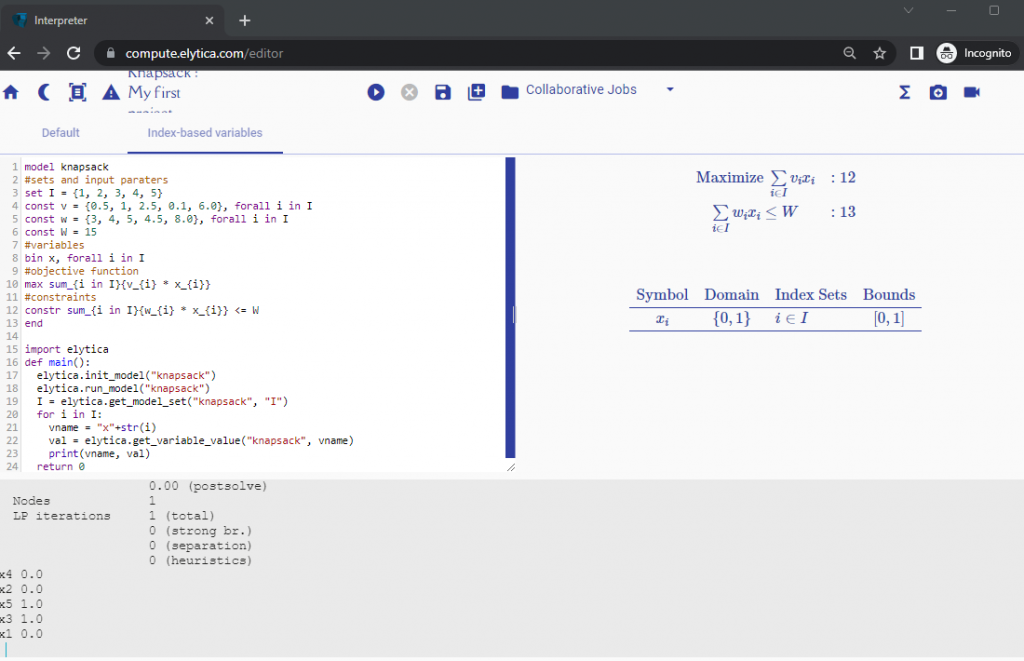
Syntax used for capturing index-based models
The remainder of this tutorial is to take you through the concepts of index sets and index-based variables. For this purpose, let us review the formulation of the standard knapsack problem. Provided as input is a list of items indexed by the set I . For each item i \in I we associate a value v_i and weight w_i. The objective of the knapsack problem is to select a subset of items from I that will maximize the total sum of the item values v_i, subject to the constraint that the total sum of the weights w_i is less or equal than a predefined capacity W.
Let the binary decision variable x_i take on a value of 1 if item i should be included in the knapsack, and 0 otherwise. Mathematically, the problem is formulated as
\text{maximize} \sum_{i \in I}{v_ix_i}
\\\text{subject to} \sum_{i \in I}{w_ix_i} \le WIt is clear that we will be dealing with the following concepts when formulating any type of optimization problem:
- Index sets – for our knapsack problem we only have the index set I.
- Decision variables – the binary variables x_i are used to indicate the inclusion/exclusion of an item
- Constants – these are the input parameters to the model, and for the knapsack problem they are v_i and w_i.
- Constraints – for our knapsack problem we only have the one constraint \sum_{i \in I}{w_ix_i} \le W, where W is also treated as a constant.
Let us go back to our newly created job and go through the details of the example.
You will recall from Tutorial 1 that optimization problems are captured in the elytica Interpreter in the space between the key words model [model_name] and end. Statements following the # symbol are treated as comments.
model knapsack
#index sets, variables, constants, and constraints defined here
endFirst, start with the necessary index sets that will be used for indexing the variables and constants. Assume we have 5 items from which to select an optimal subset for inclusion in the knapsack. Then, by using the set keyword enter the following line to your model definition
set I = {1,2,3,4,5}The next step is to define the constants. For this make use of the const keyword and relate the input data to the index set with the keyword forall.
const v = {0.5, 1, 2.5, 0.1, 6.0}, forall i in I
const w = {3, 4, 5, 4.5, 8.0}, forall i in IYou have essential created two arrays of which the elements may be accessed through the indices in the index set I. For instance, v_i with i=3 refers to the third entry in the array which is the element 2.5.
The const keyword is also used for declaring scalar constants, for instance, if we want to assign the value 15 to the capacity parameter W.
const W = 15Next, you want to declare a binary variable x_i, for all i \in I, which will take on a value of 1 if item i is included in the knapsack, and 0 otherwise.
binary x, forall i in IThe only thing to do now to complete your formulation of the knapsack problem is to add the objective function and the capacity constraint. At this point, things become a little bit more interesting. Up to now, the syntax for declaring sets, constants and variables are still very intuitive. But how do you capture an objective function, which is mathematically written as \sum_{i \in I}v_ix_i, using plain English? The answer is – use the typesetting language that millions of people all over the world use for creating mathematical documentation, namely \LaTeX !! No need to rush off and do an online course on \LaTeX. By working through this tutorial we will take you through the syntax step by step.
The objective function is identified by the maximize or minimize keywords. The abbreviations max or min will also be acceptable to the interpretation engine. Add the following line of (adapted) \LaTeX to add the knapsack objective function to the model:
max sum_{i in I}{ v_{i}*x_{i} }If you are a seasoned \LaTeX user, you will notice that the usual backslash in front of the \LaTeX statements (e.g. \sum and \in ), have been omitted. Secondly, we have to indicate to the interpretation engine which of the terms should be treated as part of the summation. That is, you need to enclose v_i x_i with curly brackets. Lastly, although we may mathematically write v_i x_i to express the product of the two variables v_i and x_i, we still need to explicitly tell the interpretation engine that this is a product by using the product operator *
For first time users of \LaTeX, a short explanation of the above line may be helpful. The syntax sum_{i in I}, tells the interpretation engine that the term to follow is a summation over the set I. This instruction will produce the symbol \sum_{i \in I} when rendered as part of the mathematical model on the right-hand side of the screen. The underscore following the variable names is used for sub-scripting the index i.
The knapsack constraint \displaystyle \sum_{i \in I}w_ix_i \le W is added to the model formulation by using the constraint (or the abbreviation constr) keyword:
constr sum_{i in I}{ w_{i}*x_{i} } <= WIf you have followed all the steps above, your model code should look like this:
model knapsack
set I = {1, 2, 3, 4, 5}
const v = {0.5, 1, 2.5, 0.1, 6.0}, forall i in I
const w = {3, 4, 5, 4.5, 8.0}, forall i in I
const W = 15
bin x, forall i in I
max sum_{i in I}{v_{i} * x_{i}}
constr sum_{i in I}{w_{i} * x_{i}} <= W
endJust like with Tutorial 1, some additional configurations are required to solve the model and to print the solution to the screen.
import elytica
def main():
elytica.init_model("knapsack")
elytica.run_model("knapsack")
I = elytica.get_model_set("knapsack","I")
for i in I:
value = elytica.get_variable_value("knapsack", f"x{i}")
print(f"x{i}", value)
return 0To print the solution values for the binary decision variables x_1, x_2, \dots, x_5, the elytica function get_variable_value() is called within a for-loop, which iterates over the index set I.
